Recherche du maximum à partir d'un sommet
En un sommet x0 du polyèdre P décrit par A·x ≤ b, on peut trouver n lignes aj de la matrice A, linéairement indépendantes, et telles que aj·s=bj (on peut trouver n faces de P dont l'intersection est x0). Notons S l'ensemble des indices j de ces lignes aj et AS la matrice inversible extraite de A formée par ces lignes . Les aj pour j ∈ S forment une base de l'espace des formes linéaires sur ℝn (vues comme vecteurs lignes), et on obtient les coordonnèes de c dans cette base par u=c·AS-1. Si u ≥ 0, alors certainement c·(x-x0)≤0 pour tout x tel que AS·(x-x0)≤0 et donc le maximum de c·x sur P est atteint en x0.
Sinon, on essaie de suivre à partir de x0 une arête le long de laquelle c·x augmente, jusqu'à un prochain sommet de P. On choisit i*, le premier i∈S tel que la coordonnée de c suivant ai soit strictement négative et on suit l'arête intersection des faces ai·x=bi pour les i∈S différents de i*. Le vecteur directeur y de l'arête (indiquant aussi le sens de parcours) est l'opposé de la colonne de AS-1 correspondant à i*. Si A·y ≤ 0, on ne sort jamais de P en suivant l'arête et comme c·x augmente le long de l'arête, il n'a pas de maximum sur P.
Sinon on va traverser les plans aj·x=bj pour lesquels aj·y>0. On s'arrête dès qu'on en traverse un, en le nouveau sommet x0+λy, avec λ le minimum des (bj-aj·x0)/aj·y pour les j avec aj·y>0. A ce nouveau sommet on associe la base donnée par l'ensemble d'indices S privé de i* et auquel on ajoute j*, le plus petit des indices j pour lesquels le minimum λ. est atteint.
On recommence avec le nouveau sommet et la nouvelle base. On peut en fait ne pas avoir changé de sommet (si λ=0), mais on a toujours changé la base. On peut montrer qu'on ne boucle pas grâce aux choix faits, et on sort toujours soit avec la réponse qu'il n'y a pas de maximum, soit avec un sommet qui maximise c·x.
Avant d'écrire la procédure qui fait ce qu'on vient d'expliquer, on écrit deux petites routines.
La première, PositifouNul, teste si un vecteur est positif ou nul, et range dans une liste les positions des composantes strictement négatives.
| > | PositifouNul:=proc(v,pos)
local i,rep,postemp; rep:=true;postemp:=[]; for i to Dimension(v) do if v[i]<0 then rep:=false; postemp:=[op(postemp),i]; end if; end do; assign(pos=postemp);rep; end proc: |
Un exemple d'utilisation:
| > | v:=Vector[row](8,rand(-2..2)); PositifouNul(v,'pos'); pos; |
![]()
![]()
![]()
La deuxième, Mini, calcule le minimum d'une liste (ça, la fonction "min" sait faire) et affecte à un nom la première position où ce minimum est atteint
| > | Mini:=proc(liste,pos)
local i, mini; mini:=liste[1];assign(pos=1); if nops(liste)>1 then for i from 2 to nops(liste) do if liste[i]<mini then mini:=liste[i]; assign(pos=i) end if end do; end if; mini; end proc: |
Un exemple d'utilisation:
| > | liste:=[seq(rand(-10..10)(),i=1..15)]; Mini(liste,'pos'); pos; |
![]()
![]()
![]()
Enfin, voici la procédure de recherche du maximum, avec en entrée les données A, b et c du problème de maximisation comme ci-dessus, un sommet x0 du polyèdre et une liste d'indice S décrivant une base attachée à ce sommet
| > | ChercheMax:=proc(A,b,c,x0,S)
local sommet,base,InvAS,n,u,possortant,liste,arete,lambda,posentrant; n:=ColumnDimension(A); sommet:=x0; base:=sort(S); InvAS:=SubMatrix(A,S,1..n)^(-1); u:=Multiply(c,InvAS); #les coordonnées de c dans la base de formes linéaires donnée par S while PositifouNul(u,'possortant')=false #tant qu'on n'est pas à un sommet qui maximise do arete:=-Column(InvAS,possortant[1]); if PositifouNul(Multiply(A,-arete),'liste') then return "pas de maximum" #l'arête continue sans sortir du polyèdre else lambda:=Mini([seq((b[liste[i]]-Multiply(Row(A,liste[i]),sommet)) /Multiply(Row(A,liste[i]),arete),i=1..nops(liste))],'posentrant'); sommet:=sommet+lambda*arete; #le nouveau sommet rencontré sur l'arête base:=sort(subsop(possortant[1]=liste[posentrant],base)); #la liste d'indices pour la nouvelle base InvAS:=MatrixInverse(SubMatrix(A,base,1..n)); u:=Multiply(c,InvAS);#coordonnées de c dans la nouvelle base end if; end do; [Multiply(c,sommet), sommet, base]; end proc: |
La procédure ci-dessus n'est certainement pas ce qu'on peut faire de mieux comme implémentation. Remarquons par exemple qu'on calcule l'inverse de la matrice AS à chaque étape. Or, les S successifs ne diffèrent que d'un élément, et donc deux matrices AS successives ne diffèrent que d'une ligne. Il serait donc nettement plus économique de calculer l'inverse de AS à partir de l'inverse calculée à l'étape précédente!. Vous pouvez essayer de modifier la procédure pour prendre cette remarque en compte.
Voici un exemple d'éxécution. On cherche le maximum de x+y+z avec x,y,z ≥ 0, x,z ≤ 1 et 3x+2y+z ≤ 3. On part de l'origine, avec la base donnée par les trois premières contraintes. L'utilisation de "trace" permet de suivre la progression dans les sommets. On voit qu'on reste coincé un certain temps au même sommet, mais qu'on s'en sort tout de même. La réponse comprend la valeur du maximum, le sommet trouvé où il est atteint, et les indices de la base associée (ce dernier renseignement sera utile plus loin).
| > | A:=Matrix([[-1,0,0],[0,-1,0],[0,0,-1],[1,0,0],[0,0,1],[3,2,1]]);
b:=Vector([0,0,0,1,1,3]) ; c:=Vector[row]([1,1,1]); x0:=Vector(3,0); S:=[1,2,3]; trace(ChercheMax): ChercheMax(A,b,c,x0,S); untrace(ChercheMax): |
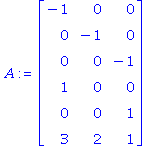
](images_simplex/simplex_8.gif)
![]()
](images_simplex/simplex_10.gif)
![]()
{--> enter ChercheMax, args = Matrix(6, 3, {(1, 1) = -1, (1, 2) = 0, (1, 3) = 0, (2, 1) = 0, (2, 2) = -1, (2, 3) = 0, (3, 1) = 0, (3, 2) = 0, (3, 3) = -1, (4, 1) = 1, (4, 2) = 0, (4, 3) = 0, (5, 1) = 0, (5, 2) = 0, (5, 3) = 1, (6, 1) = 3, (6, 2) = 2, (6, 3) = 1}), Vector(6, {(1) = 0, (2) = 0, (3) = 0, (4) = 1, (5) = 1, (6) = 3}), Vector[row](3, {(1) = 1, (2) = 1, (3) = 1}), Vector(3, {(1) = 0, (2) = 0, (3) = 0}), [1, 2, 3]
![]()
](images_simplex/simplex_13.gif)
![]()
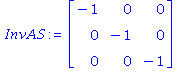
![]()
](images_simplex/simplex_17.gif)
![]()
](images_simplex/simplex_19.gif)
![]()
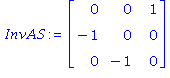
![]()
](images_simplex/simplex_23.gif)
![]()
](images_simplex/simplex_25.gif)
![]()
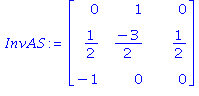
![]()
](images_simplex/simplex_29.gif)
![]()
](images_simplex/simplex_31.gif)
![]()
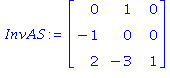
![]()
](images_simplex/simplex_35.gif)
![]()
](images_simplex/simplex_37.gif)
![]()
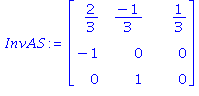
![]()
](images_simplex/simplex_41.gif)
![]()
](images_simplex/simplex_43.gif)
![]()
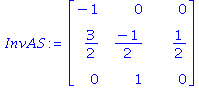
![]()
, [1, 5, 6]]](images_simplex/simplex_47.gif)
<-- exit ChercheMax (now at top level) = [2, Vector(3, {(1) = 0, (2) = 1, (3) = 1}), [1, 5, 6]]}
, [1, 5, 6]]](images_simplex/simplex_48.gif)
Vérifions qu'on trouve bien la même chose avec la fonction toute faite du paquet "simplex":
| > | simplex[maximize](x+y+z,{x<=1,z<=1,3*x+2*y+z<=3},NONNEGATIVE); |
![]()