Trouver un sommet d'où partir
La procédure ChercheMax suppose qu'on connaît déjà un sommet. Nous allons voir qu'elle peut être utilisée pour trouver un sommet où démarrer. Nous supposons ici le polyèdre P donné par les inégalités x≥0, A·x≤b, où x est un vecteur colonne à n composantes, A une matrice m×n et b un vecteur colonne à m composantes. Nous verrons plus loin comment se ramener dans tous les cas à des variables non négatives.
Soit b1 le vecteur extrait de b en ne retenant que les composantes ≥0, b2 l'opposé de celui formé par les composantes strictement négatives de b (on a donc b2 >0). On note A1 la matrice extraite de A en choisissant les lignes correspondant aux composantes de b1, A2 l'opposé de celle extraite de A en choisissant les lignes correspondant aux composantes de b2. Les inégalités A·x≤b se réécrivent donc A1·x≤b1, A2·x≥ b2. Soit mi le nombre de lignes de Ai, et notons ai,j les lignes de Ai.
On introduit un nouveau vecteur variable y à m2 composantes, et on considère le problème de maximisation de 1·(A2·x-y) (où 1 est le vecteur ligne à m2 composantes 1), avec les contraintes x≥0, y≥0, A1·x≤b1, A2·x-y≤b2. Les données de ce problème s'écrivent matriciellement ainsi:
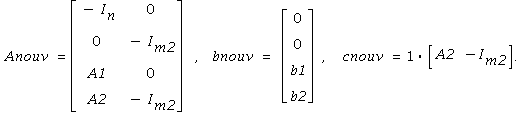
Ce nouveau problème a clairement une solution car 1·(A2·x-y) est majoré par 1·b2 sur le polyèdre défini par les contraintes, et que ce dernier est non vide puisque l'origine en est un sommet (avec une base donnée par les n+m2 premières contraintes de positivité des variables).
Ceci permet de rentrer le problème de maximisation dans ChercheMax, qui nous rend la valeur M du maximum de 1·(A2·x-y), un sommet (x0,y0), et une base T associée à ce sommet. Si M est strictement inférieur à 1·b2, le polyèdre P est vide.
Si M=1·b2, alors x0 est un sommet de P et on obtient une base S associée à ce sommet avec
- les contraintes xi ≥ 0 figurant dans T,
- les contraintes a1j·x ≤ b1j figurant dans T
- et les contraintes -a2j·x ≤ -b2j telles que yj≥0 figure dans T (a2,j·x-yj≤ b2,j y figure aussi).
Il ne reste plus qu'à écrire ce qu'on vient d'expliquer sous forme de procédure.
| > | Sommet:=proc(A,b)
local m,n, listeneg, listepos,m1,m2,A1,A2,b1,b2,p,q, Anouv,bnouv,cnouv,inter,sommet,base,i; m:=Dimension(b); n:=ColumnDimension(A); PositifouNul(b,'listeneg'); listepos:=convert({seq(i,i=1..m)} minus convert(listeneg,set),list); m1:=nops(listepos); m2:=nops(listeneg); A1:=SubMatrix(A,listepos,1..n); A2:=-SubMatrix(A,listeneg,1..n); b1:=SubVector(b,listepos); b2:=-SubVector(b,listeneg); q:=n+m2; p:= q+m; Anouv:=Matrix(p,q); bnouv:=Vector(p); Anouv[1..q,1..q]:=-Matrix(q,q,shape=identity); Anouv[q+1..q+m1,1..n]:=A1; Anouv[q+m1+1..p,1..n]:=A2; Anouv[q+m1+1..p,n+1..q]:=-Matrix(m2,m2,shape=identity); bnouv[q+1..q+m1]:=b1; bnouv[q+m1+1..p]:=b2; cnouv:=Multiply(Vector[row](m2,1),Anouv[q+m1+1..p,1..q]); inter:=ChercheMax(Anouv,bnouv,cnouv,Vector(q,0),[seq(i,i=1..q)]); if inter[1]< add(b2[i],i=1..m2) then return "pas faisable" else sommet:=SubVector(inter[2],1..n); base:=[]; for i to n do if member(i,inter[3]) then base:=[op(base),i] end if end do; for i from n+1 to q do if (member(i,inter[3]) and member(i+m,inter[3])) then base:=[op(base),n+listeneg[i-n]] end if end do; for i from q+1 to q+m1 do if member(i,inter[3]) then base:=[op(base),n+listepos[i-q]] end if end do end if; sommet,base; end proc: |
Voyons un exemple d'éxécution:
| > | A:=Matrix(4,3,rand(-5..5)); b:=Vector(4,rand(-5..5)); Sommet(A,b); |
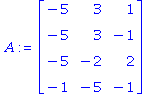
](images_simplex/simplex_52.gif)
, [5, 6, 7]](images_simplex/simplex_53.gif)
Dans le résultat qui est donné pour la base, les numéros 1, 2, 3 correspondent aux conditions de positivité sur les variables. Les lignes de A sont comptées à partir de 4.
| > |